What This Chapter Is About

Uninformed Search Techniques

• Depth First Search
• Breadth First Search
• Depth First Search

Informed Search Techniques

• Hill Climbing
• Best First Search
• Greedy Search
• A* Search
• MiniMax Search
• Alpha Beta Procedure

Problem Solving Using Search

What is Problem Solving?

Generating solutions from observed data

Problem

- Set of Goals

- Set of Objects

- Set of Operations

Problem Space

All valid states using operations on objects

Search

- Search for solution in problem space

- Example: DFS, BFS,...

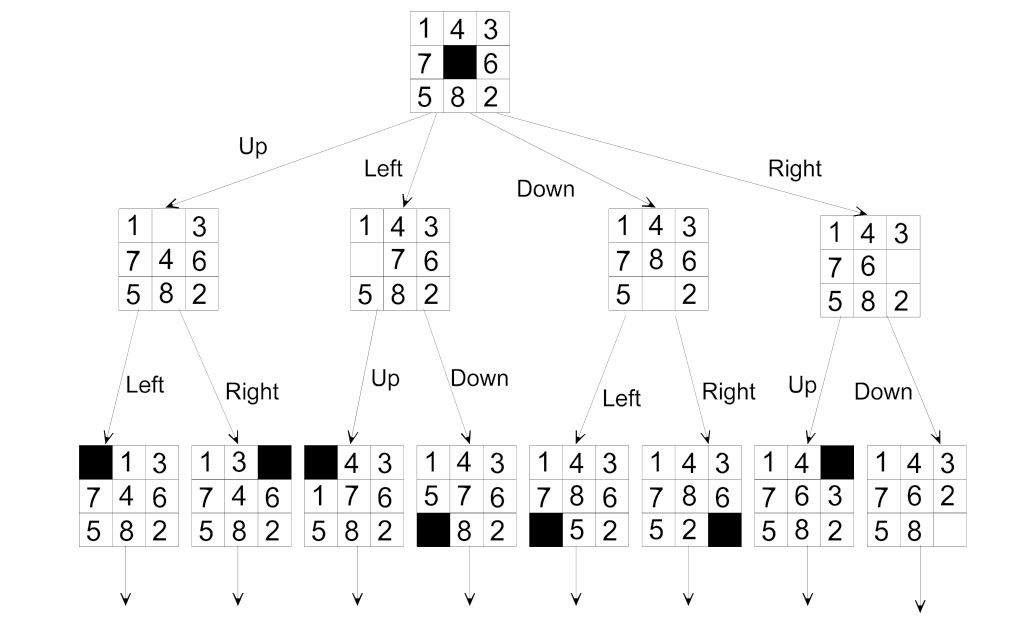
8 Puzzle

N Queen

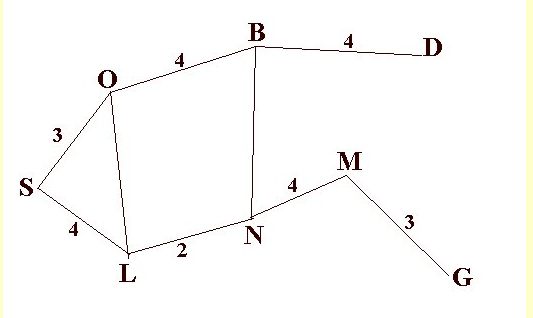
Path Finding

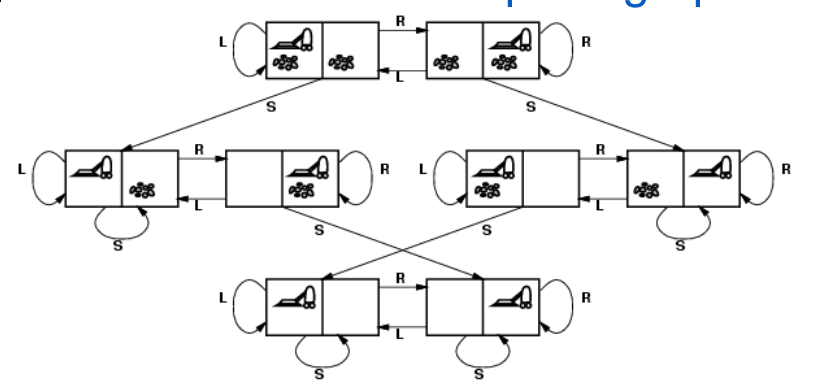
Tower of Hanoi

Actions: PICKUP, PUTDOWN, FORWARD, BACKWARD, LEFT, RIGHT

Condition-1: Only top ring can be moved at a time

Condition-2: Smaller ring cannot be below the large one

Graph Search

- Direct Graph

- Start from Initial State

- Use operations

- Check Goal State

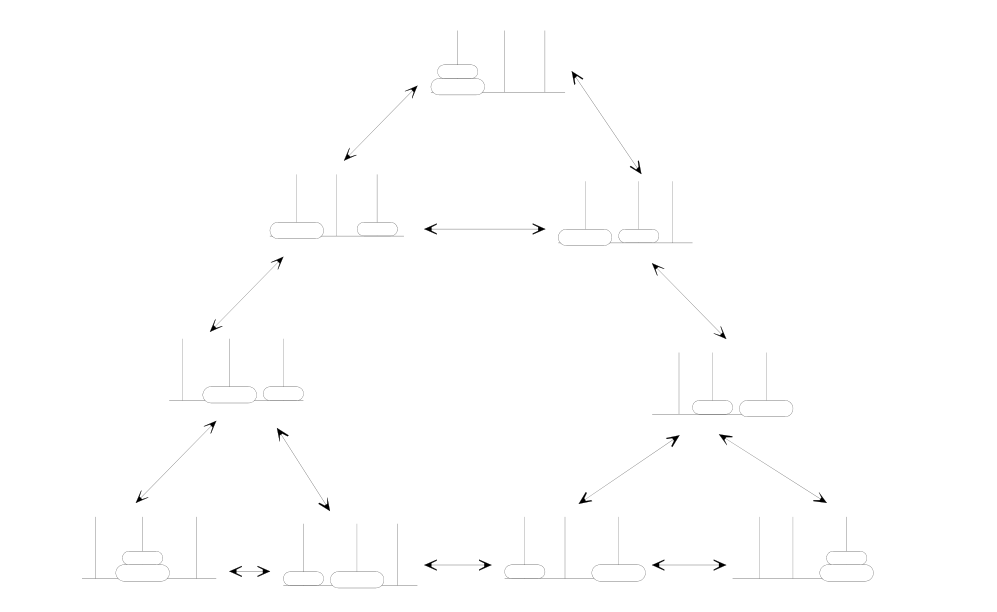
Tower of Hanoi State Space Representation

8-Puzzle State Space Representation

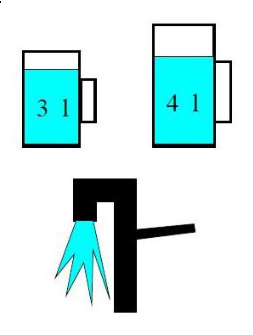
Example: Water Jug Problem

Uninformed Search

- Blind Search

- Only Problem Defintion

- No idea if one non-goal state is better than other

Blind Search

- Visit all the nodes in a a certain order for pre-defined goal

- No cleverness

- No guarantee of reaching goal state

Less Ineffective than Informed Search

Path Finding Problem

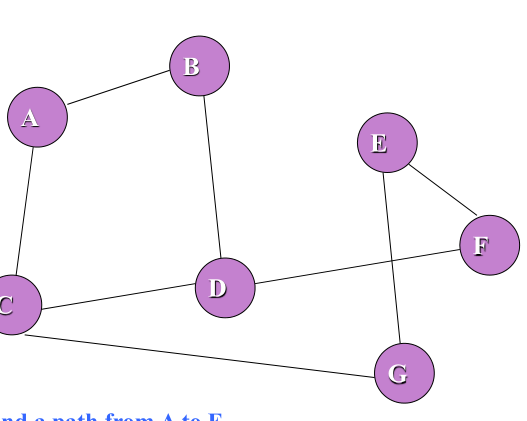
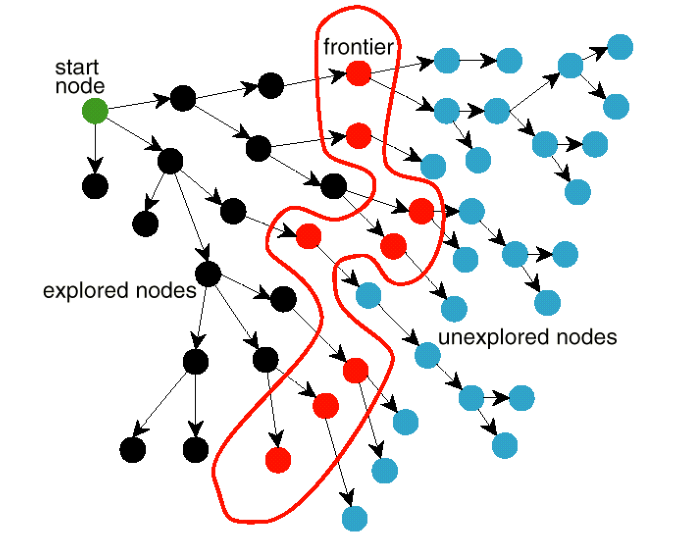
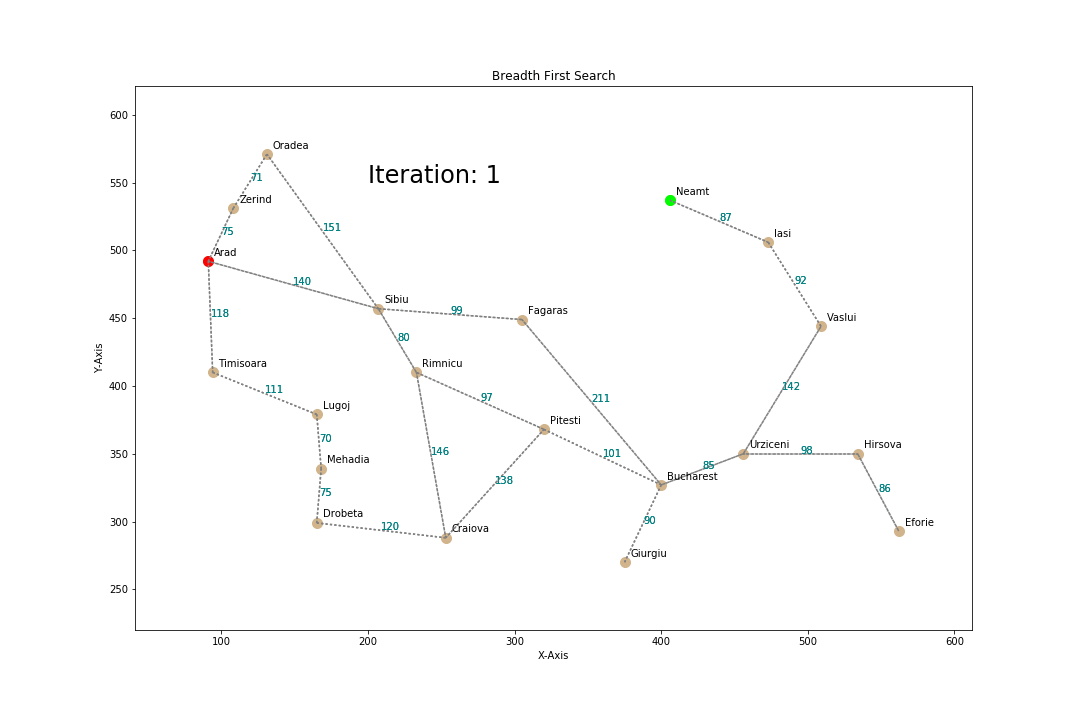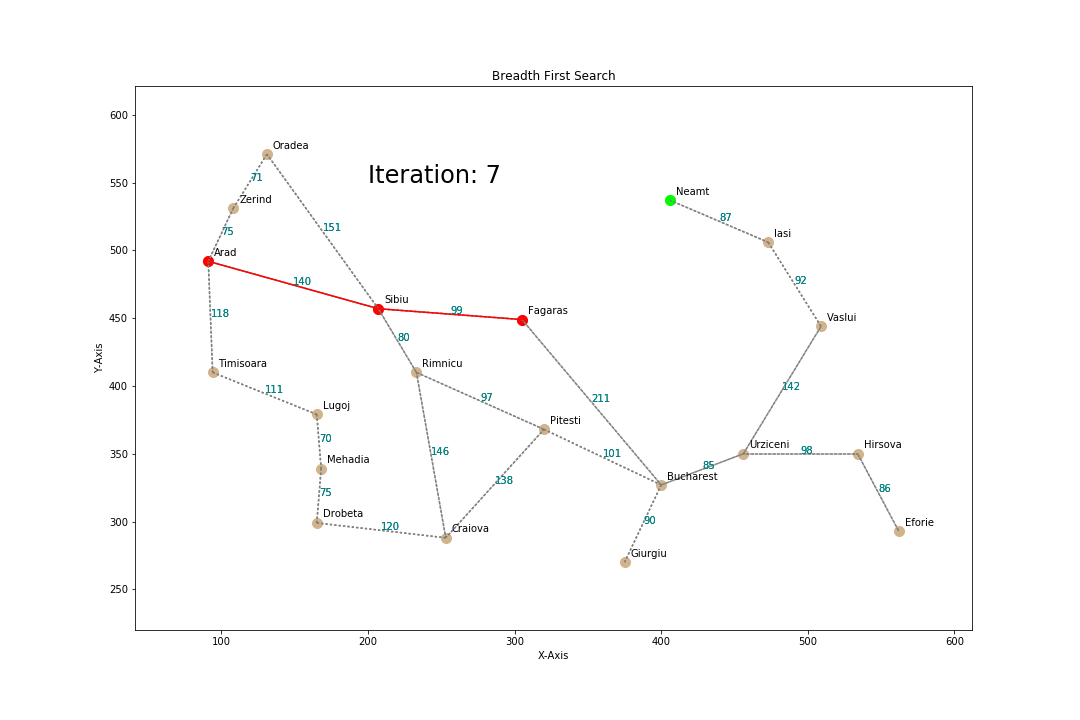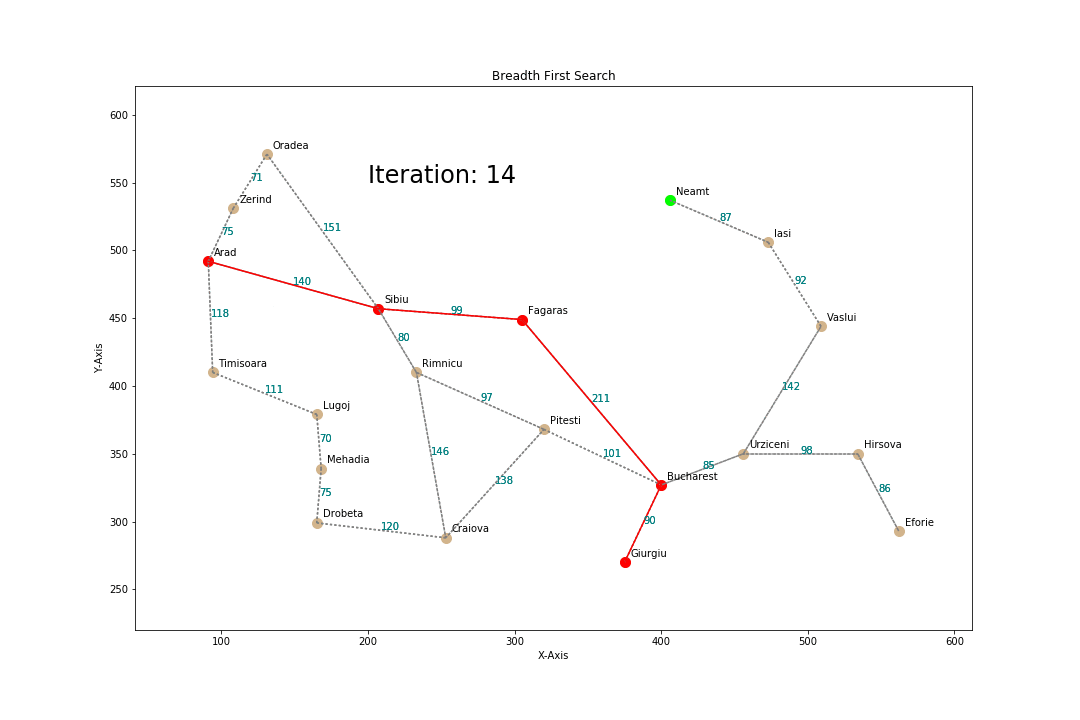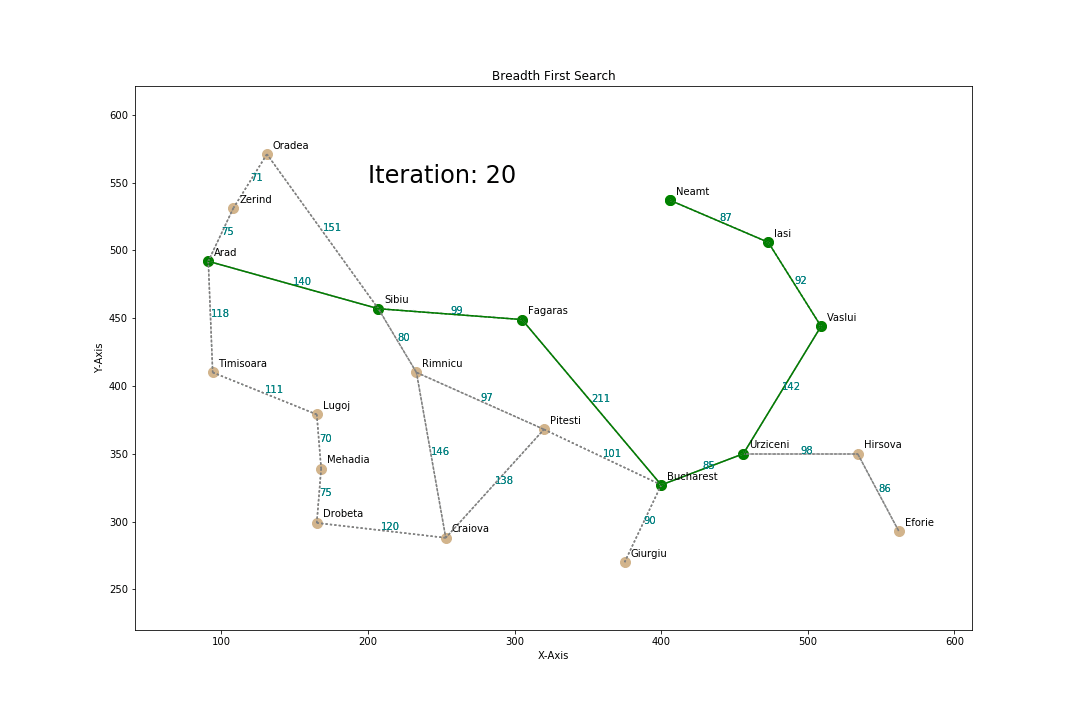
Breadth First Search

How?

- Proceed level by level down the tree

- Start from root node and explore all the children, left to right

How?

- If no solution found, expand the first(leftmost) child, then second at same depth,...

BFS

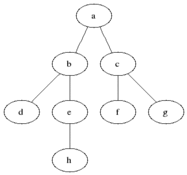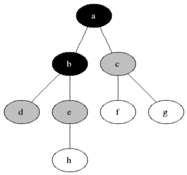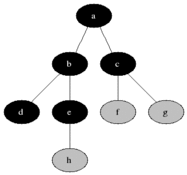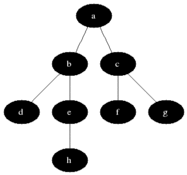
BFS

Algorithm

- Place start node at the end of queue

- Examine the node at the front of queue, then

• if queue is EMPTY, STOP
• if node is GOAL state, STOP
• else ADD the children of the node to the end of the queue

Algorithm

1. Place the starting node on the queue
2. If queue is EMPTY return FAILURE and STOP
3. If first element on the queue is GOAL node, STOP
4. Otherwise, remove and expand the first element from the queue and place all the children at the end of the queue
5. Goto step 2

Data Structure?

Queue

Properties

Complete? Yes! Always reaches GOAL

Time? O(b^d):: Number of nodes generated

Space? O(b^d):: Keeps every node in the memory

Optimal? Yes! except deeper solutions

Branching Factor=b and goal found at depth=d

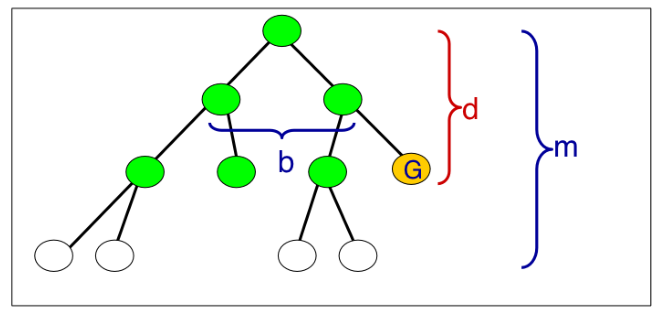
Disadvantages?

Space is more problem than time.

Depth First Search

How?

- Proceed down a single branch at a time

- Expand root node, then leftmost child of the root, then leftmost child of that node,..

DFS

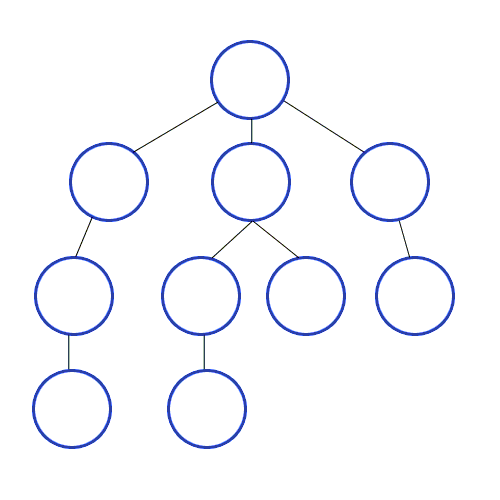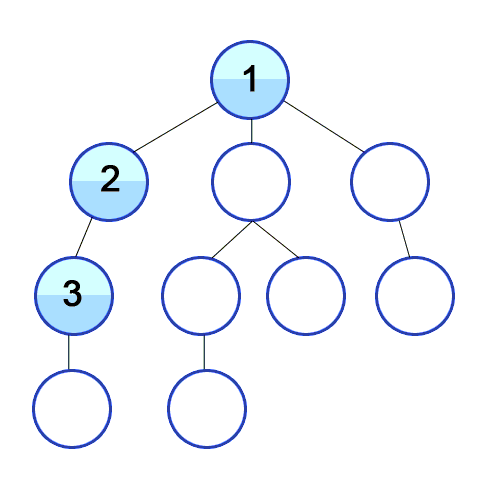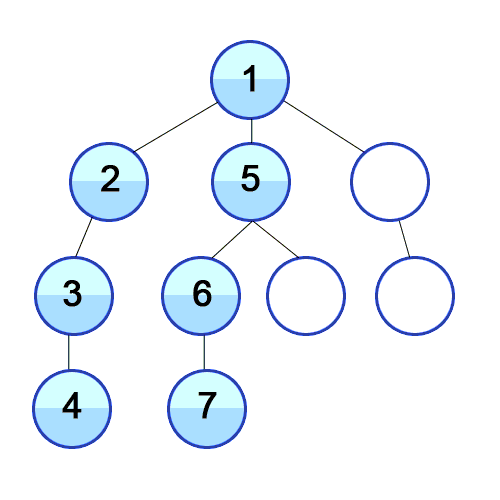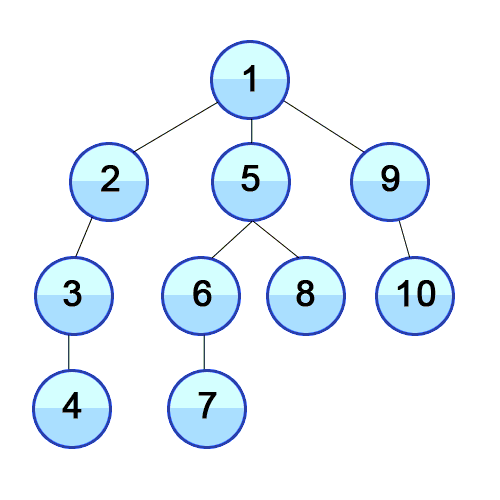
DFS

Data Structure?

Stack (LIFO)

Algorithm

1. Place the starting node on the stack
2. If staack is EMPTY return FAILURE and STOP
3. If top element on the stack (pop operation) is GOAL node, STOP
4. Otherwise, remove and expand the top element from the stack and push the children to stack
5. Goto step 2

Properties

Complete? No! Fails in infinite depth :: A-B-C-A

Time? O(b^m):: Maximum depth

Space? O(b*m):: Linear Space

Optimal? NO! except deeper solutions

Disadvantages?

Can go to wrong branch and may take very long time to find solution

Depth-Limited Search

- Optimized DFS

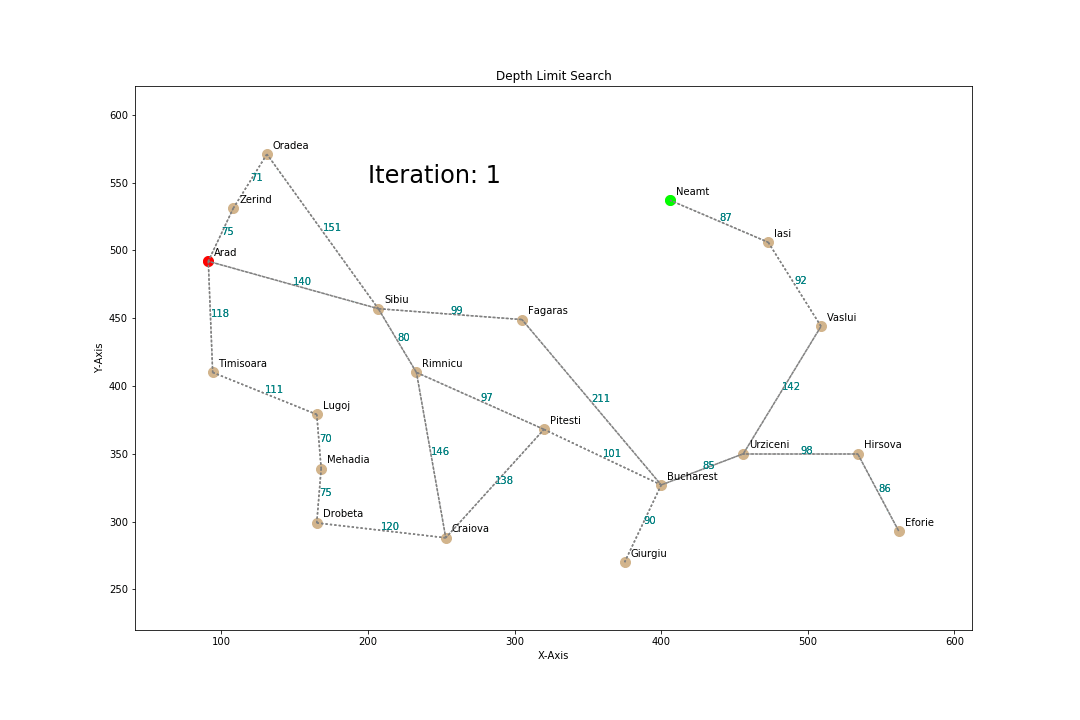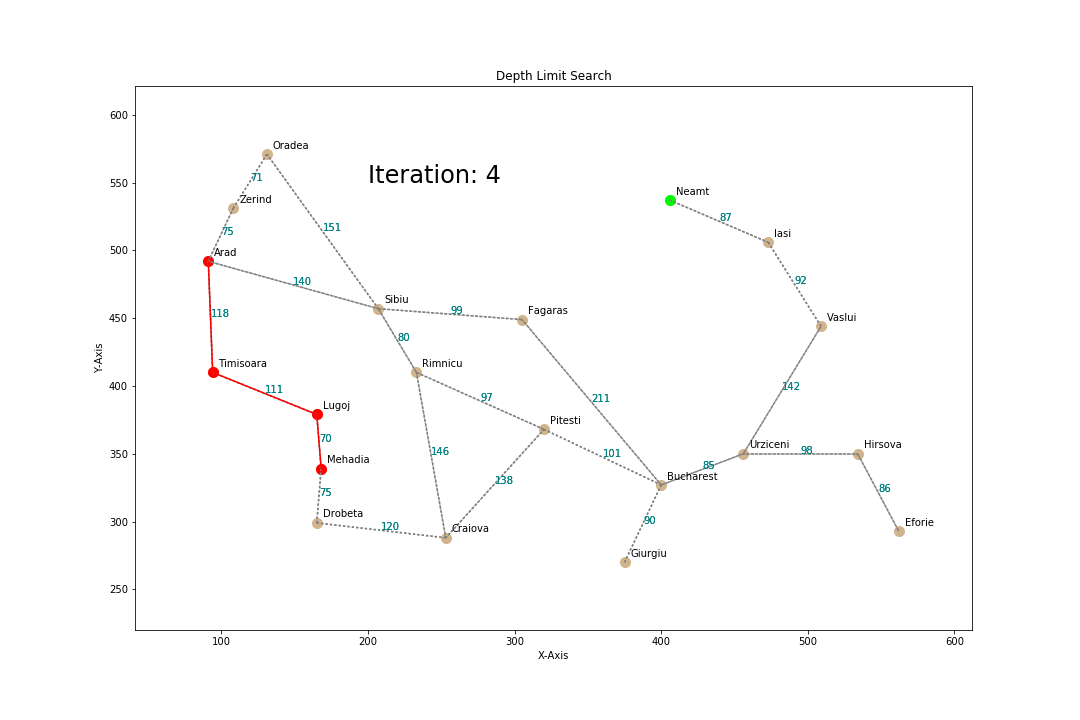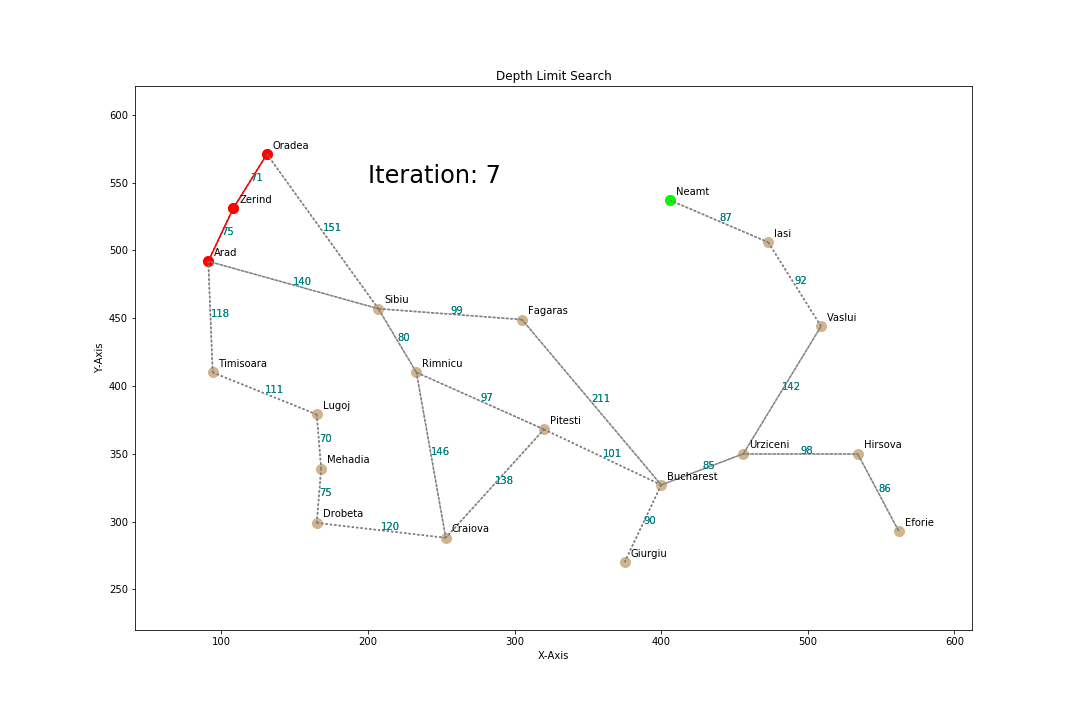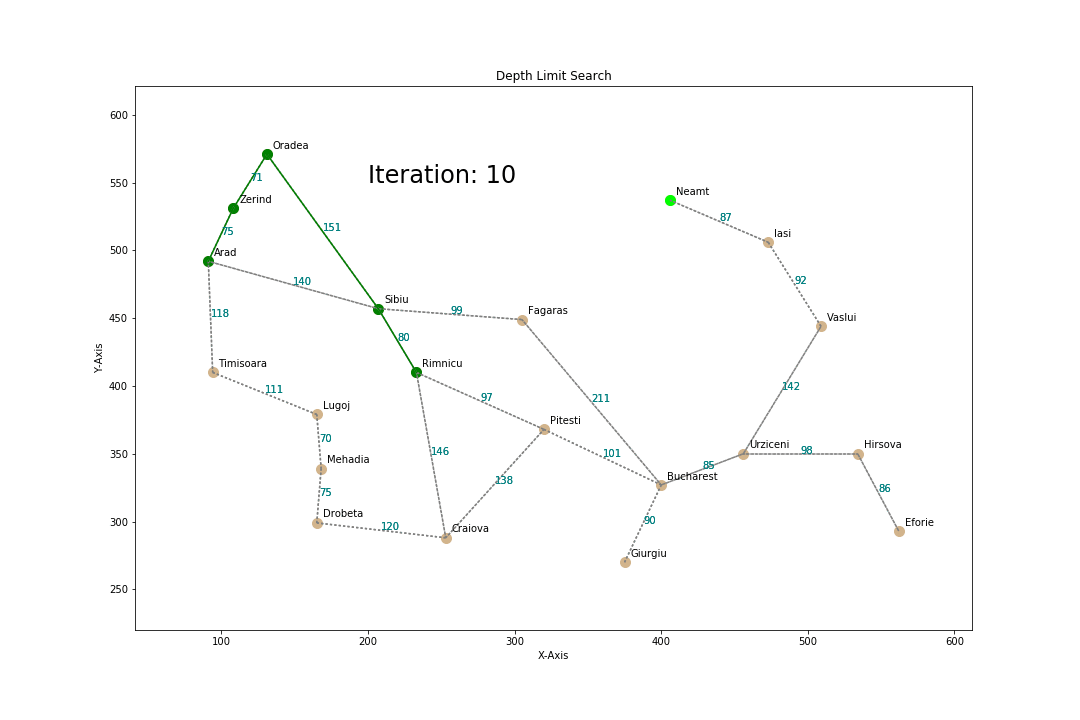
How?

- Perform DFS but only at a specified depth L

- The path length is at max L

Properties

Complete? No! Solution may be beyond depth level

Time? O(b^L):: Maximum depth

Space? O(b*L):: Linear Space

Optimal? NO!

Informed Search

- Domain Specific Information

- Heuristic Function h(n) : Goodness of a node n

Heuristic Function

h(n) = estimated cost of minimal cost path from n to goal state

Best First Search

- Uses evaluation function f(n) to select a node for expansion

- Node with lowest evaluation function is expanded first

Use an evaluation function for each node -> desirability

1. Start with initial node and put into priority queue
2. Pick the best node from the queue
3. Generate its successor
4. For each successor do:
   - if it haas not been generated before then evaluate it and add to queue
   - if it has been generated before, then change the parent and if this new path is better, update the cost of getting to its any successor node
   - if the goal step is found or no more node in the queue then STOP
5. Go to step 2

Types of Best First Search

- Greedy Best First Search

- A* Search

Greedy Best First

- tries to get as close as it can to the goal

- expands the node that appears closest to the goal

- Uses only heuristic function

Evaluation function h(n) = estimate of cost from n to closest goal

Example: hsld(n) = straight-line distance from n to goal

f(n) = h(n)

h(n) = 0 for goal state

Properties

Complete? NO! Can get stuck in loops

Time? O(b^m):: depends on good heuristic

Space? O(b^m):: Keeps all nodes in memory

Optimal? NO!

A*

evaluation function f(n) = g(n) + h(n)

g(n) = cost so far to reach n

estimated cost from n to goal

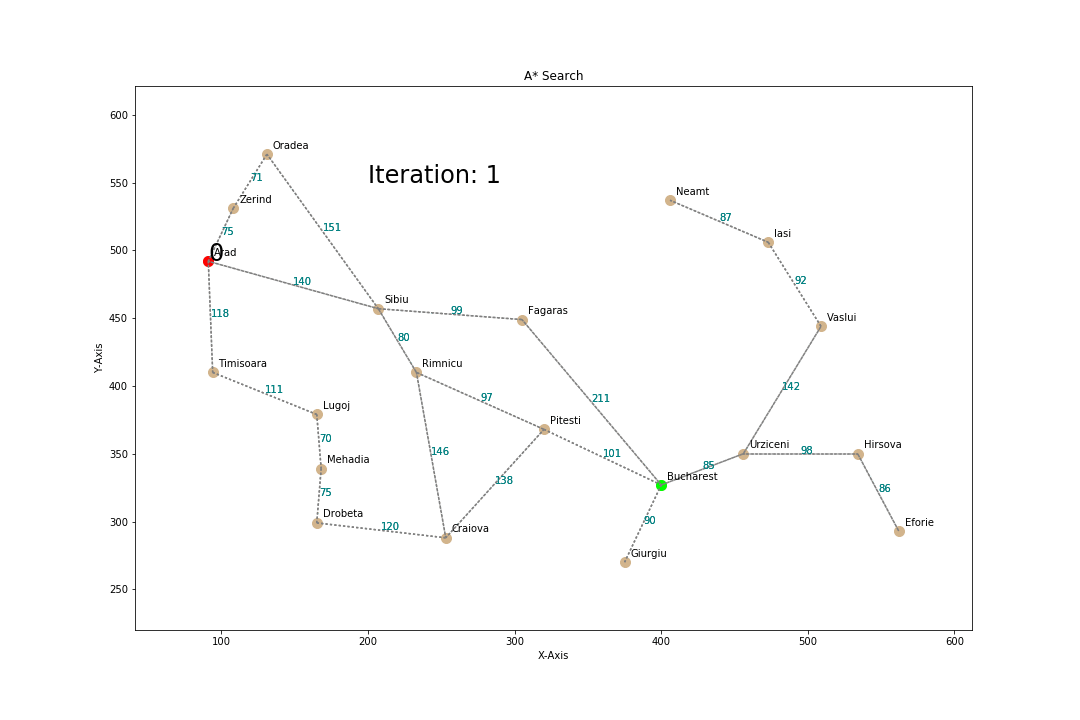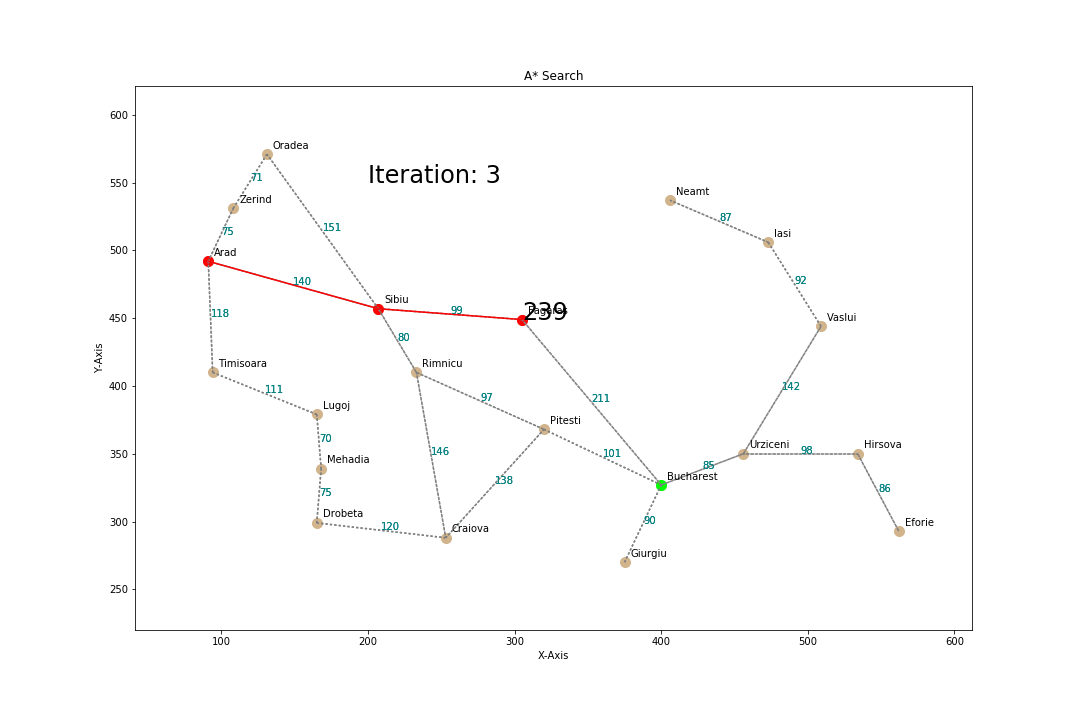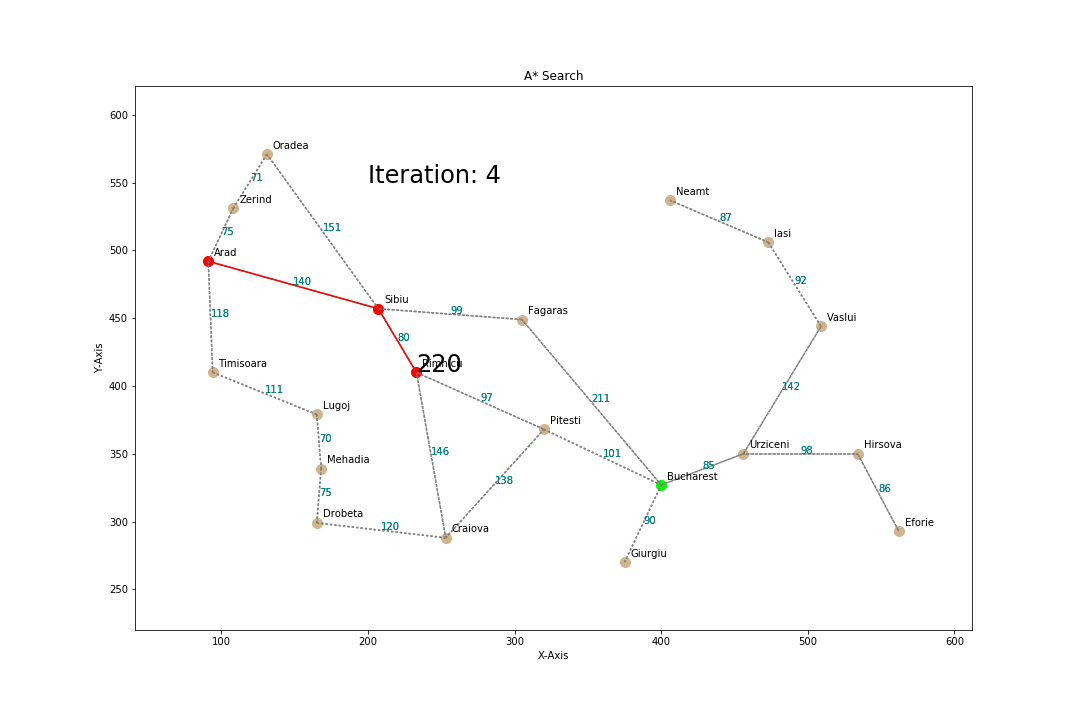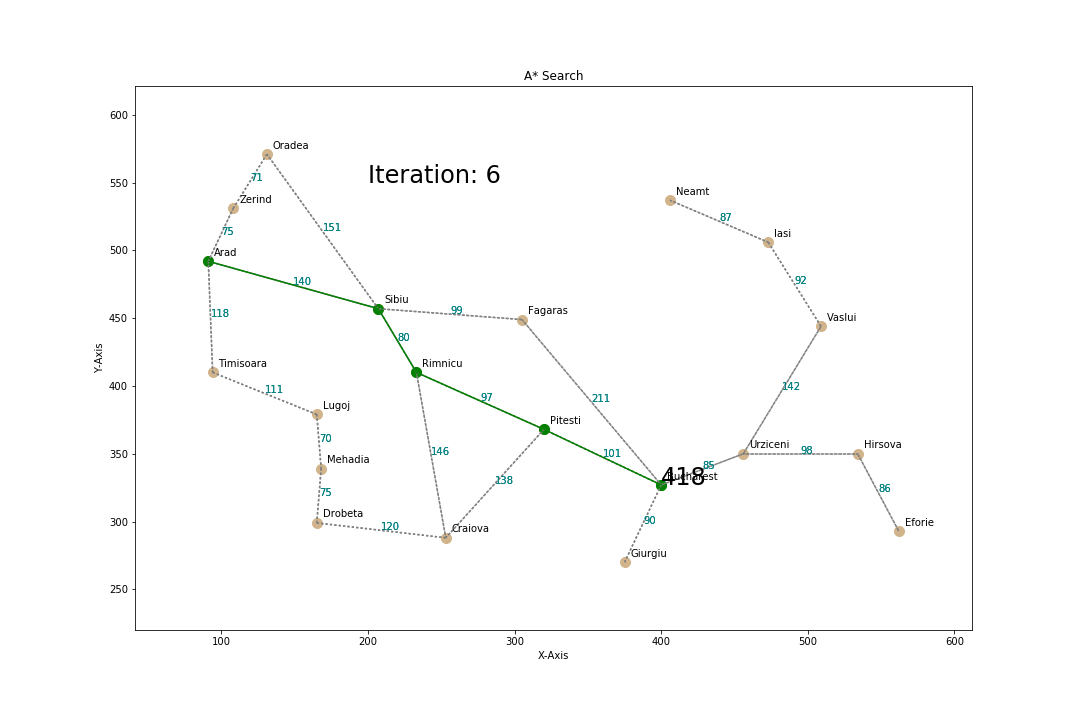
Properties

Complete? YES!

Time? Exponential

Space? Keeps all nodes in memory

Optimal? YES!

Hill Climbing

Adverserial Search

Competitive Environments in which the agents goals are in conflict

- Often known as games

Game

- Initial State

- A successor function

- A terminal test

- A Utility function

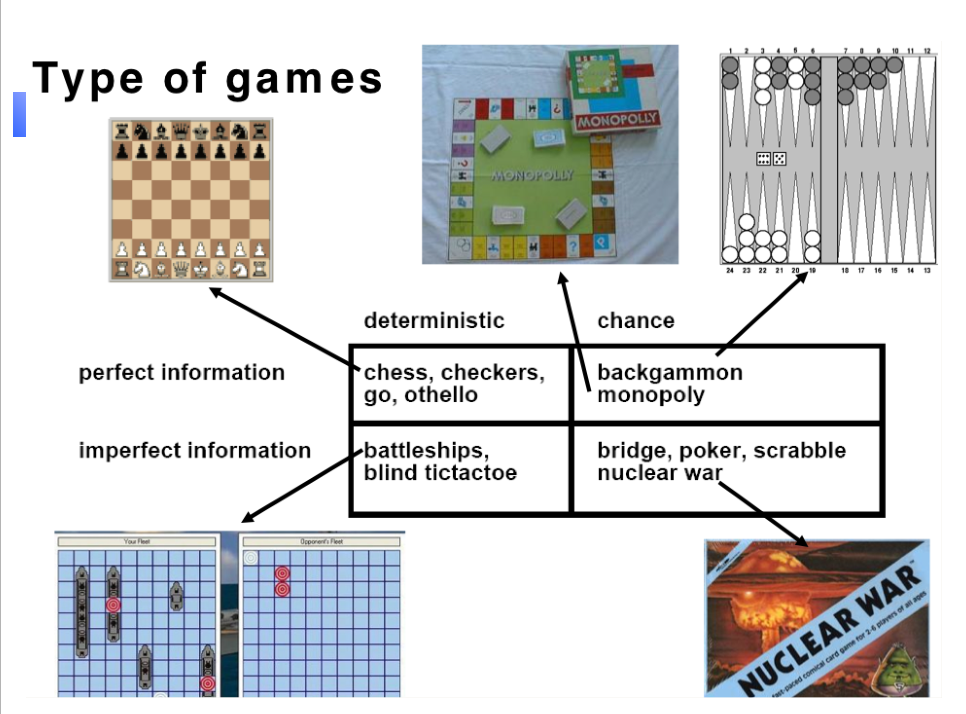
Adverserial

Opposition between agent's Utility functions

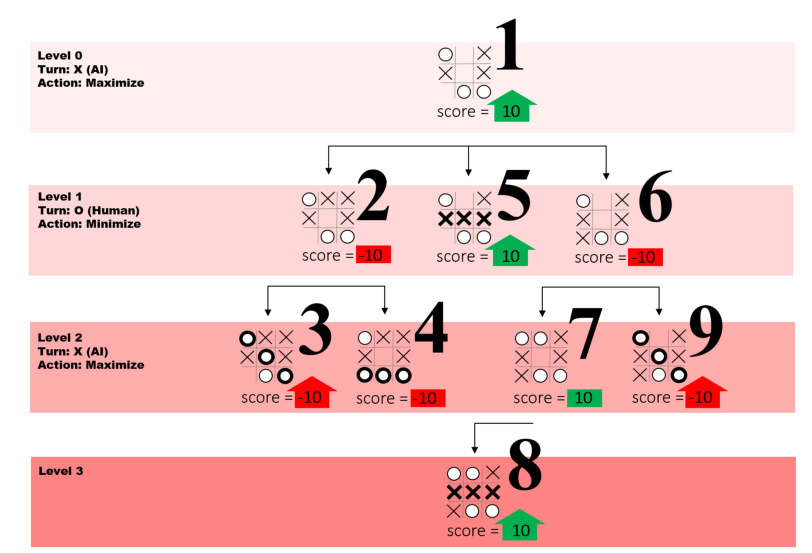
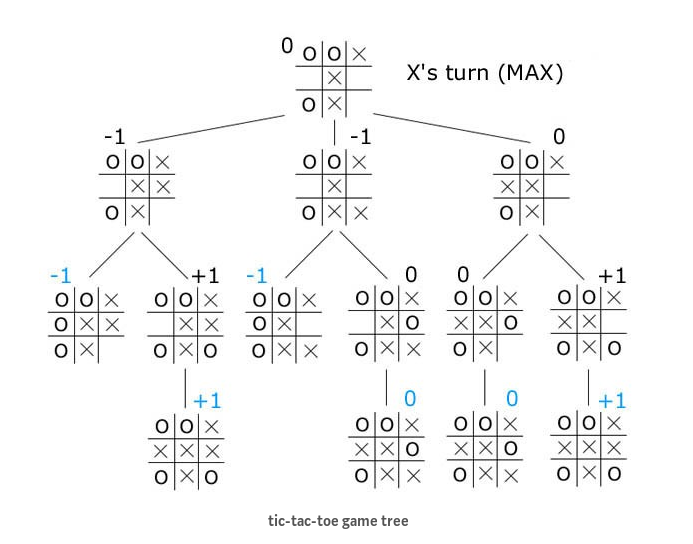
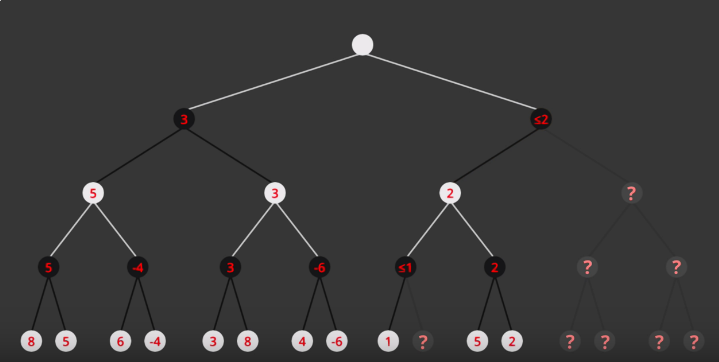
MiniMax

- depth first search with limited depth

- Static evaluation function for all leaf nodes

- assume opponent will make the best move possible

Algorithm

Algorithm

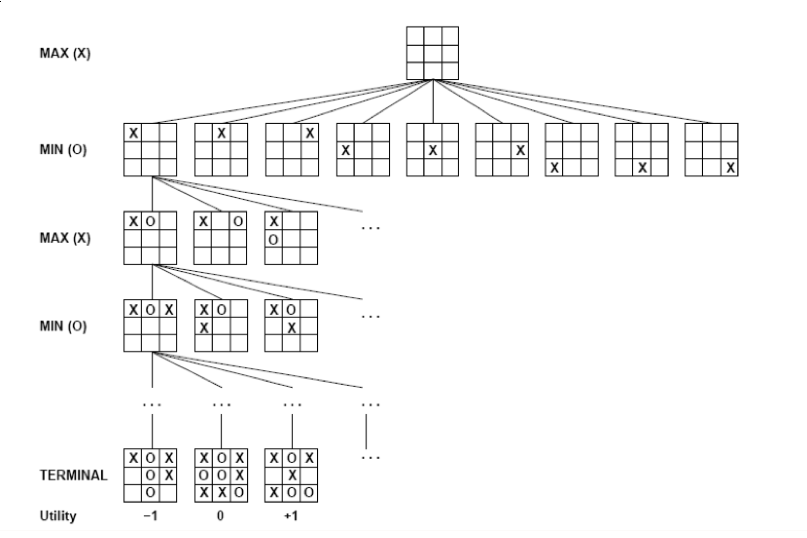
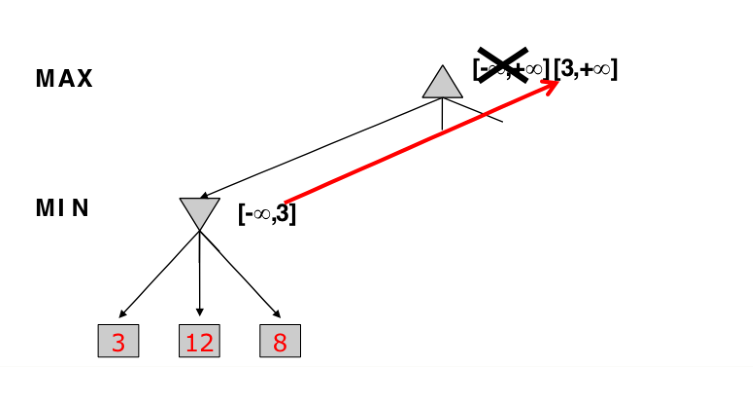
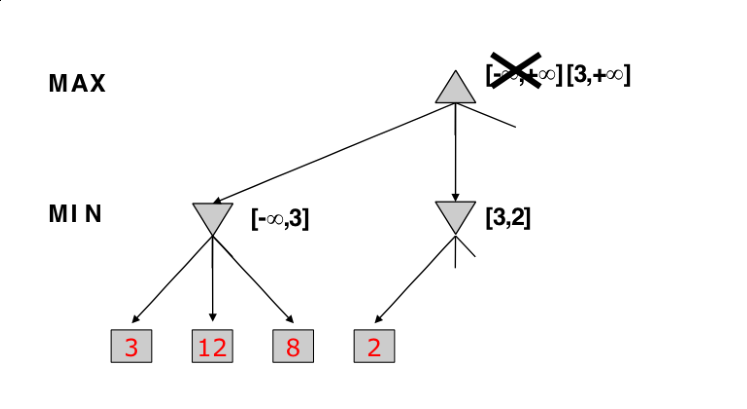
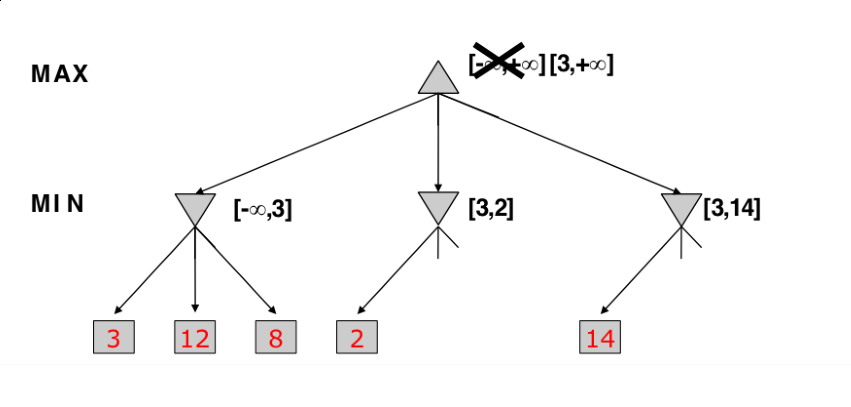
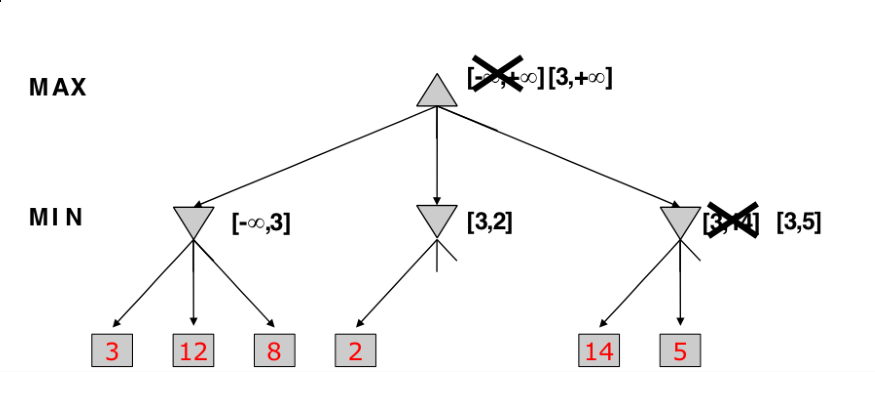
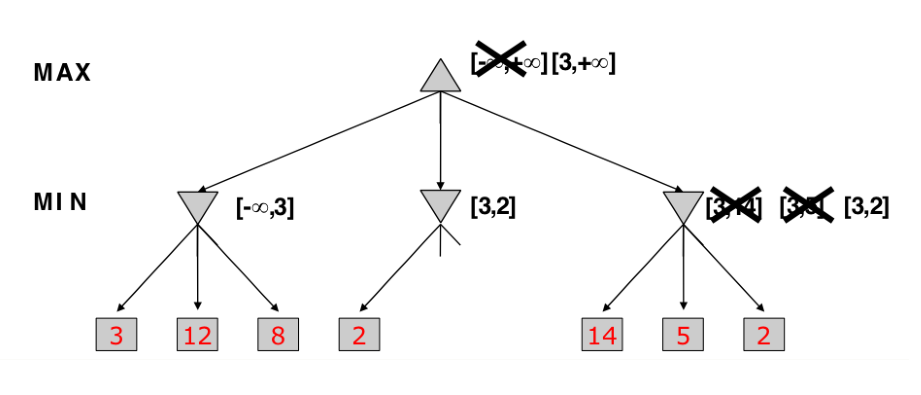
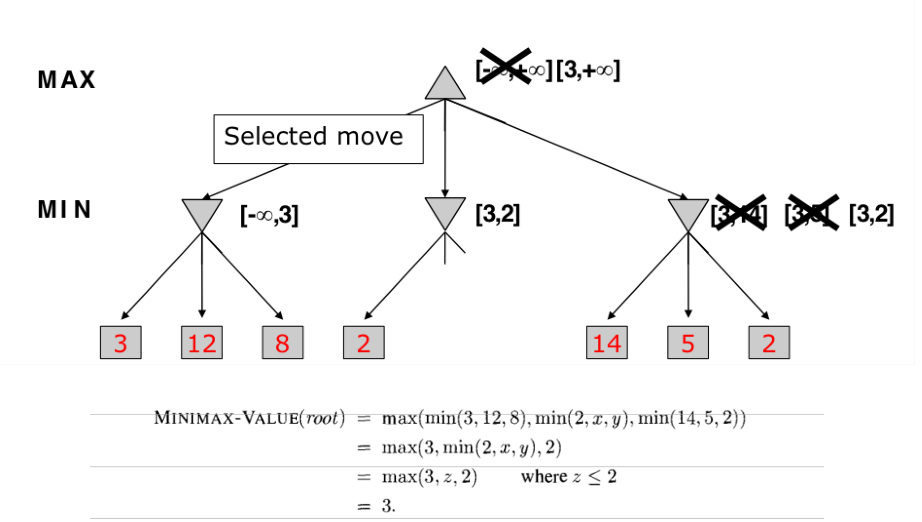
Alpha-Beta Pruning

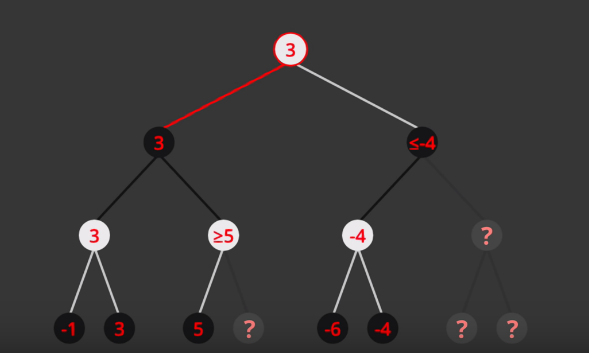
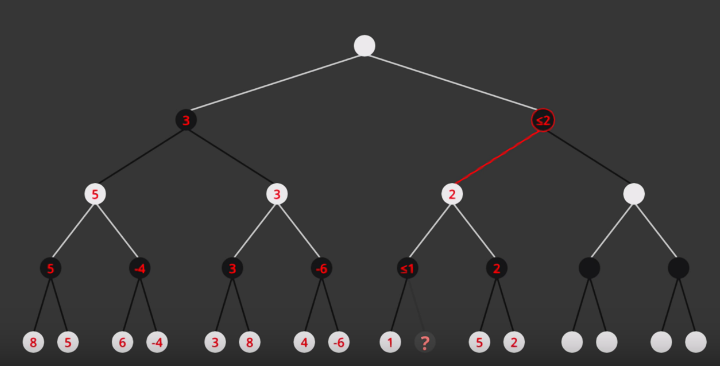
- Optimized MiniMax

- Instead of expanding nodes, we try to infer based on node values

- Depends on the order on how nodes are expanded

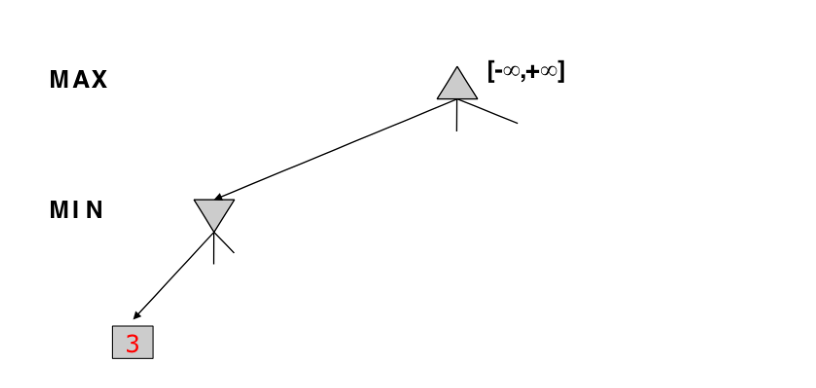
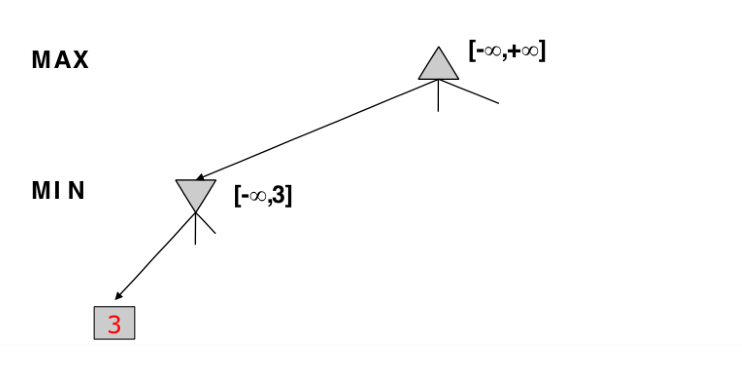
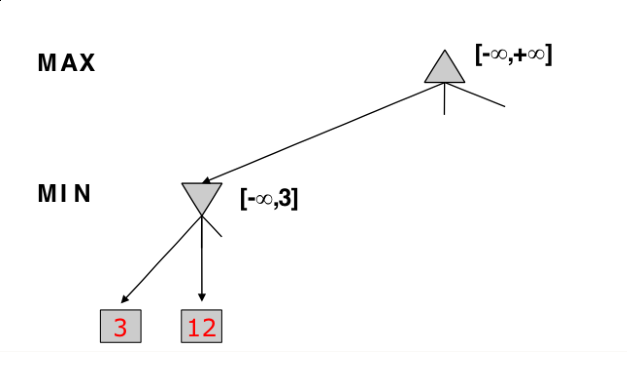
Alpha -> value of best choice so far for MAX (highest value)

Beta -> value of best choice so far for MIN (lowest value)

Each node keeps track of [alpha, beta]

Initial value

Alpha -> -INF

Beta -> +INF

Simple Pruning